From what I read, starting with a cube makes it easier for the students to associate the shape to the equation. I think it would be helpful to also have manipulatives for them to build and measure. One page had an example of using sugar cubes...though I'm sure students would love that...I think that having a class that energized would be a unique experience I'm not sure I want to have!
How to find the volume of a cube or a rectangular box of tissues
Volume of a Box
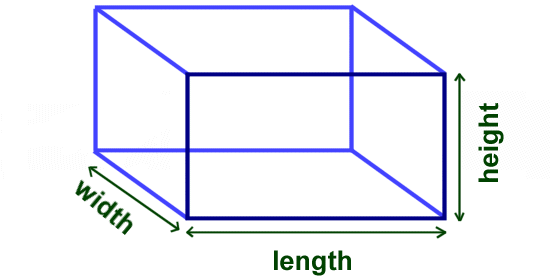
Volume= l x w x h
So if our box of tissues was 10 inches long, 4 inches wide and 3 inches wide we would have the equation 10x4x3=120. For the area of a box, it doesn't matter what number is multiplied first, the sum will be the same.
Volume of a Cylinder
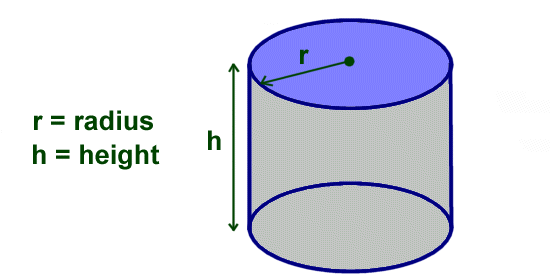
Volume = πr2h
The formula to find the volume of a cylinder is similar to that of a cube because you are using multiplication. The big difference is that you are using the radius squared as well as π, two numbers that students might be less familiar or apprehensive using.
The equation we would use is 3.14 x radius x radius x height so if our cylinder has a radius of 4 inches and a height of 6 inches we would have the equation 3.14 x 4 x 4 x 6= 301.44.
Volume of a Cone
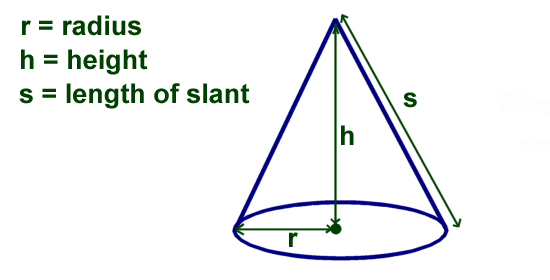
Volume = 1/3πr2h
Now, we have to change things up a bit when we get to the volume of a cone and do some division! We also can use the Pythagorean Therum to find the slant, pretty cool stuff! The equation we would use is very similar to the one we used to find the volume of a cylinder with the important addition of division, 3.14 x radius x radius x height÷3
Math Joke of the Week:
Q: How do you make one vanish?
A: Add a 'g' to the beginning and it's gone!

No comments:
Post a Comment