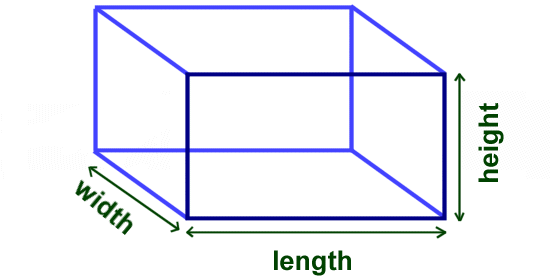
This video from Khan Academy was pretty interesting on the topic of area and perimeter in general.
While I was relearning this topic I found it really cool that a square is also called a special rectangle. I had never heard this before, we just had to remember that a square is also a rectangle. I thought that having the 'special' affixed to the square was a great way for students to remember that even though it has 4 equal sides, it's not just a square, it's a rectangle too. The 'special' is that keyword that triggers their memory that the square fits in two categories
Now, back to perimeter vs area. On this site I found a fabulous explanation of why a rectangle that has the same perimeter doesn't have the same area:
Area vs. Perimeter of RectanglesDate: 03/19/2000 at 16:19:30 From: Melissa Subject: Perimeter and area I don't understand how two rectangles with exactly the same perimeter can enclose different areas. Can you explain that to me? Thank you, Melissa Date: 03/19/2000 at 23:15:36
From: Doctor Peterson
Subject: Re: Perimeter and area
Hi, Melissa.
I can start by convincing you that it's really true. A mathematician
often looks at a question like this by thinking about the extreme
cases, to get a feel for how far things can go. So let's think about
extreme rectangles.
Suppose you make a loop of string, say 24 inches long, and try to make
a rectangle of it, by putting four fingers into the loop and moving
them around. What's the widest rectangle you can make? Pull your
fingers as far as they can go, and you'll have something like this:
________________
(O________________O)
If you imagine your fingers having no width, you can see that the
widest rectangle possible would have zero height (or as little as you
are willing to have and still call it a rectangle) and width 12
inches. Its area will be zero.
At the other extreme, of course, you can stretch your rectangle
vertically so that it is 12 inches high with no width, and again has
zero area. Yet you know that in between you do have a positive area,
and in fact it will turn out that a square (with the width and height
the same) will have the greatest area you can make.
So how can area change when the perimeter stays the same?
Here's one way to look at it, suggested by a problem someone sent in
recently. Let's reverse the question and try to build a rectangle out
of 12 one-inch squares (a fixed area) and see why we won't always get
the same perimeter. The 12 squares will have a total perimeter of 48
inches (4 inches each). If I line up the squares in a row, only two or
three sides of each square will be part of the perimeter, while the
others will be shared with neighbors:
_ _ _ _ _ _ _ _ _ _ _ _
|_|_|_|_|_|_|_|_|_|_|_|_|
Each of the 11 "interior edges" between two squares takes away two
inches from the perimeter (one side of each square), so the perimeter
of this rectangle will be 48 - 22 = 26. Since the height is 1 and the
width is 12, that's right: 1 + 12 + 1 + 12 = 26.
Now let's stack the squares closer together, in two rows of 6:
_ _ _ _ _ _
|_|_|_|_|_|_|
|_|_|_|_|_|_|
Now there are 16 interior edges, because more of the squares are
touching, so we subtract not 22 but 32 inches from the perimeter,
which is now 48 - 32 = 16. Yes, this is 2 + 6 + 2 + 6.
Now let's lump them even closer together (more squarish), as a 3 x 4
rectangle:
_ _ _ _
|_|_|_|_|
|_|_|_|_|
|_|_|_|_|
Now there are 17 interior edges, so the perimeter is 48 - 34 = 14
inches, which is equal to 3 + 4 + 3 + 4.
Do you see what's happening? The more squarish the rectangle is, the
more edges the squares share, and the less they contribute to the
perimeter, so the less the perimeter will be.
The same sort of thing happens with three-dimensional shapes, and this
effect is important in such questions as how your body dissipates
heat: if we picture our squares as cells, then a flat shape will let
each cell be close to the surface and cool itself off, while a
roundish shape will force more cells into the interior, where they
won't be part of the surface, and also won't lose heat easily. Lumpy
things have less "outside" for the same amount of "inside." (That's
why elephants have thin ears, to radiate more heat, and why cactuses
have thick stems, to retain more moisture.)
So the basic answer to your question is that area measures the
"inside" of a shape and perimeter measures the "outside," and by
changing the shape we can move outside parts to the inside without
changing the outside. Or, if we keep the perimeter the same as you
originally asked, we can keep the same "outside" but pack more
"inside" into it, which will puff it up.
Thanks for the question - it's fun to think about this sort of thing!
- Doctor Peterson, The Math Forum
http://mathforum.org/dr.math/
|